Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2026
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
2.
Se lanza una piedra hacia arriba desde la parte superior de un edificio en un ángulo de $30,0^{\circ}$ con la horizontal y con una velocidad inicial de 20,0 $\mathrm{m} / \mathrm{s}$. El punto de liberación está a $45,0 \mathrm{~m}$ respecto de la superficie de la Tierra. Considere despreciable la resistencia del aire.
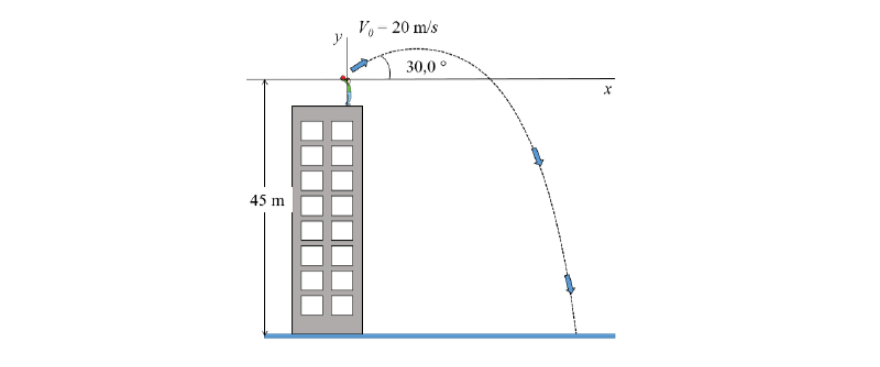
a) ¿Cuánto tiempo le toma a la piedra golpear la superficie de la Tierra?

a) ¿Cuánto tiempo le toma a la piedra golpear la superficie de la Tierra?
Respuesta
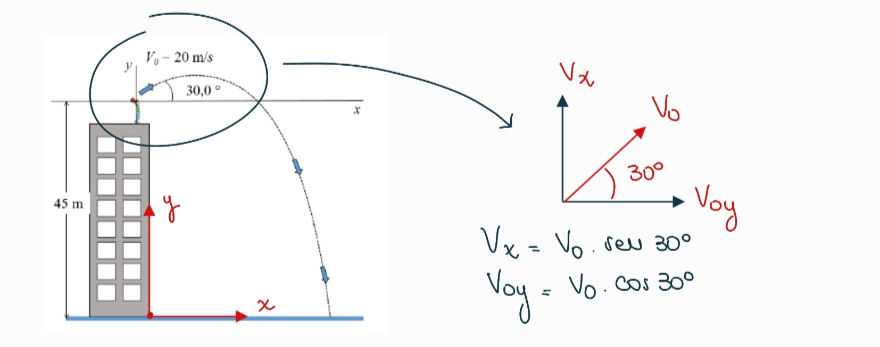
Tenemos por acá otro típíco problema de tiro oblicuo 😉 Ya tenemos un lindo esquema que nos hicieron en el enunciado, solamente le voy a agregar el sistema de referencia elegido (ah, y de paso ya te muestro también cómo queda descompuesto el vector velocidad inicial $V_0$)
Reportar problema

Las componentes $x$ e $y$ de la velocidad inicial nos quedarían así:
$V_{x} = V_0 \cdot \cos(\theta) = 20.0 \, \frac{m}{s} \cdot \cos(30^{\circ}) = 17.3 \, \frac{m}{s}$
$V_{0y} = V_0 \cdot \sin(\theta) = 20.0 \, \frac{m}{s} \cdot \sin(30^{\circ}) = 10 \, \frac{m}{s}$
Ahora sí, nos armamos las ecuaciones de movimiento para el eje $x$ y el eje $y$
👉 Eje x: MRU
$x(t) = V_{x} \cdot t$
$x(t) = 17.3 \, \frac{m}{s} \cdot t$
👉 Eje y: MRUV
Para la posición en $y$ en función del tiempo:
$y(t) = y_0 + V_{0y} \cdot t + \frac{1}{2} \cdot a \cdot t^2$
$y(t) = 45.0 \, \text{m} + 10.0 \, \frac{m}{s} \cdot t - 4.9 \, \frac{m}{s^2} \cdot t^2$
Y para la velocidad en $y$ en función del tiempo:
$V_y(t) = V_{0y} + a \cdot t$
$V_y(t) = 10.0 \, \frac{m}{s} - 9.8 \, \frac{m}{s^2} \cdot t$
Vamos entonces con la primera pregunta...
➡️ ¿Cuánto tiempo le toma a la piedra golpear la superficie de la Tierra? (o sea, el piso 😅)
Para saber cuánto tiempo le toma a la piedra golpear el piso, necesitamos encontrar el instante $t$ en el que la posición $y(t)$ es igual a cero. Para eso planteamos $y(t) = 0$ y despejamos...
$45.0 \, \text{m} + 10.0 \, \frac{m}{s} \cdot t - 4.9 \, \frac{m}{s^2} \cdot t^2 = 0$
Mirala con cariño, sacale las unidades por un ratito (tenemos todo en el sistema internacional, así que ese $t$ que estamos buscando nos va a quedar en la unidad segundos) y nos damos cuenta que tenemos una cuadrática igualada a cero:
$-4.9t^2 + 10.0t + 45.0 = 0$
Aplicamos la resolvente y, quedándonos únicamente con la solución positiva (la que tiene sentido, porque $t$ es mayor a cero) llegamos a $t = 4.22 \text{ s}$
Por lo tanto, el tiempo que le toma a la piedra golpear el piso es de $4.22 \, \text{s}$.
🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
