Tenemos por acá un problema de tiro vertical. Como siempre, arrancamos eligiendo nuestro sistema de referencia, a partir del cual vamos a escribir después las ecuaciones de movimiento. Fijate que, como el cuchillo sale de la mano del malabarista y regresa de nuevo ahí, al elegir nuestro sistema de coordenadas nos va a convenir poner el origen (o sea, los $0$ metros) justo donde están las manos del malabarista.
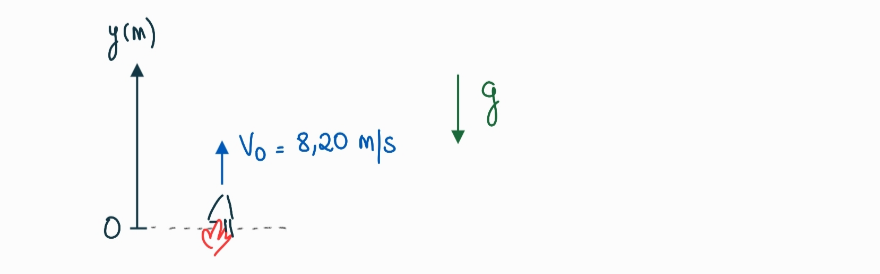
Si, eso es una mano sostenido un cuchillo jajaja en FADU no paso el CBC 😅
Con este sistema de referencia, los datos que tenemos son:
-> Velocidad inicial del cuchillo ($v_0$) = $+8.20 \mathrm{~m/s}$ (es positiva porque el cuchillo se lanza hacia arriba, en el sentido positivo de $y$)
-> Posición inicial del cuchillo ($y_0$) = $0 \mathrm{~m}$ (porque se lanza desde la mano, que es nuestro origen).
-> Aceleración de la gravedad ($g$) = $-9.8 \mathrm{~m/s^2}$ (que es negativa en nuestro sistema de referencia)
Las ecuaciones de posición $y(t)$ y de velocidad $v(t)$ nos quedan así:
$y(t) = 8.20 \mathrm{~m/s} \cdot t + \frac{1}{2} (-9.8 \mathrm{~m/s^2}) \cdot t^2$
$v(t) = 8.20 \mathrm{~m/s} -9.8 \mathrm{~m/s^2} \cdot t$
Sabemos que el cuchillo regresa a la mano del malabarista cuando su posición $y(t)$ vuelve a ser $0 \mathrm{~m}$. Así que, vamos a usar la ecuación de posición y plantear que $y(t) = 0$.
$8.20 \mathrm{~m/s} \cdot t + \frac{1}{2} (-9.8 \mathrm{~m/s^2}) \cdot t^2 = 0$
Ecuación correctamente planteada, todo en el sistema internacional, le saco las unidades por un instante para dedicarnos tranqui al despeje, sabiendo que el tiempo lo vamos a obtener en segundos.
$8.20 \cdot t - 4.9 \cdot t^2 = 0$
Tenemos una cuadrática igualada a cero, podemos aplicar la resolvente o, como en este caso $c=0$, también la podemos resolver sacando factor común $t$
$t \cdot (8.20 - 4.9 \cdot t) = 0$
Esta ecuación nos da dos posibles soluciones para $t$:
-> $t = 0 \mathrm{~s}$ (claro, eso ya lo sabíamos, el cuchillo inicialmente está en $y = 0$)
-> $8.20 - 4.9 \cdot t = 0$ (esta es la solución que buscamos!)
Despejando obtenemos que $t = 1.67 \text{ s}$ (quedándome con tres cifras significativas, si fuera el parcial lo reporto así)
Entonces, el cuchillo tardó $1.67$ segundos en volver a la mano del malabarista ☺️

