Volver a Guía
Ir al curso
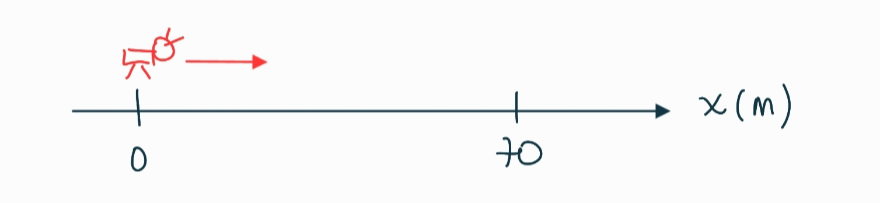
Reportar problema
CURSO RELACIONADO
Física 03
2026
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
3.
Un antílope que viene corriendo con aceleración constante tarda $7,00 \mathrm{~s}$ en pasar por dos puntos que se encuentran separados entre sí $70,0 \mathrm{~m}$. Su rapidez al pasar por el segundo punto es $15,0 \mathrm{~m} / \mathrm{s}$.
a) ¿Qué rapidez tenía al pasar por el primer punto?
a) ¿Qué rapidez tenía al pasar por el primer punto?
Respuesta
Sabemos que nuestro antílope está haciendo un MRUV (porque está corriendo con aceleración constante). Según los datos que nos dan en el enunciado, vamos a elegir nuestro sistema de referencia -> En el primer punto voy a poner mi origen de coordenadas (o sea, los $0$ metros) y cuando pasa por esa posición prendemos el cronómetro.
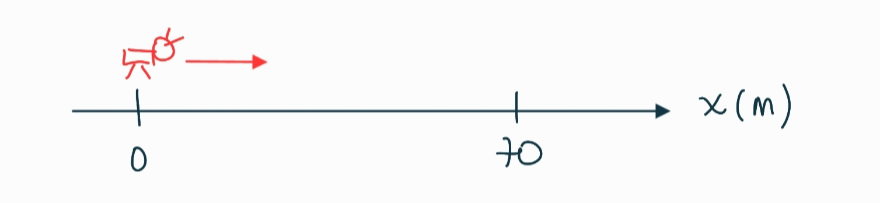
Con esta elección $x_0 = 0 \text{ m}$, $t_0 = 0 \text{ s}$ y las ecuaciones que nos hablan de la posición y la velocidad del antílope en función del tiempo nos quedarían así:
Posición en función del tiempo
$x(t) = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2$
Velocidad en función del tiempo
$v(t) = v_0 + a \cdot t$
Entonces, mirá con atención nuestras ecuaciones. Tenemos dos incógnitas ahí, $v_0$ (que es la velocidad inicial, la velocidad al pasar por el primer punto, que es lo que nos preguntan en este primer ítem) y la aceleración $a$ (que nos lo preguntan en el segundo)
Veamos qué datos tenemos...
👉 Por un lado, sabemos que el antílope tardó $7$ segundos en llegar de un punto al otro. Así que, en nuestro sistema de referencia, el antílope está en la posición $70$ metros a los $7$ segundos. Es decir, conocemos la posición en un cierto instante de tiempo, vamos a reemplazar eso en la ecuación $x(t)$
$x(t) = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2$
$v_0 \cdot 7 \text{ s} + \frac{1}{2} \cdot a \cdot (7 \text{ s})^2 = 70 \text{ m}$
Perfecto, esta ecuación me la guardo en el bolsillo, es una ecuación que relaciona nuestras dos incógnitas, $a$ y $v_0$.
👉 Además, sabemos que la velocidad al pasar por el segundo punto es de $15 \, \frac{m}{s}$. Es decir, conocemos la velocidad a los $7$ segundos, vamos a reemplazar eso en la ecuación de $v(t)$
$v(t) = v_0 + a \cdot t$
$v_0 + a \cdot 7 \text{ s} = 15 \, \frac{m}{s}$
Geniaaaal, acá tenemos otra ecuación que nos relaciona ambas incógnitas! Nos armamos entonces este sistema de dos ecuaciones con dos incógnitas, $a$ y $v_0$:
$\begin{cases} v_0 \cdot 7 \text{ s} + \frac{1}{2} \cdot a \cdot (7 \text{ s})^2 = 70 \text{ m} \\ v_0 + a \cdot 7 \text{ s} = 15 \, \frac{m}{s} \end{cases}$
Tenemos ecuaciones correctamente planteadas y todas las unidades en el sistema internacional, como venimos haciendo en las clases, voy a sacarle las unidades por un ratito sólo para centrarnos tranqui en la resolución del sistema, sabiendo que la aceleración la vamos a obtener en $\frac{m}{s^2}$ y $v_0$ en $\frac{m}{s}$.
El sistema a resolver, ya sin las unidades, nos queda así:
$\begin{cases} 7 \cdot v_0 + \frac{1}{2} \cdot a \cdot 7^2 = 70 \\ v_0 + 7 \cdot a = 15 \end{cases}$
¿Más amigable ahora, no?
Para resolverlo, yo voy a elegir este camino, pero vos podrías tomar otro y llegar a los mismos resultados. De la ecuación (2) (la de abajo) voy a despejar $v_0$
$v_0 + 7 \cdot a = 15$
$v_0 = 15 - 7 \cdot a$
Y lo reemplazo en la ecuación (1) (la de arriba)
$7 \cdot v_0 + \frac{1}{2} \cdot a \cdot 7^2 = 70$
$7 \cdot (15 - 7 \cdot a) + \frac{1}{2} \cdot a \cdot 7^2 = 70$
Hago distributiva...
$105 - 49 \cdot a + \frac{49}{2} \cdot a = 70$
$- 49 \cdot a + \frac{49}{2} \cdot a = 70 - 105$
$-\frac{49}{2} \cdot a = -35$
$a = 1.43 \, \frac{m}{s^2}$
Perfecto, ya tenemos la aceleración. Ahora reemplazamos este resultado para obtener la velocidad $v_0$
$v_0 = 15 - 7 \cdot a$
$v_0 = 15 - 7 \cdot 1.43 \, \frac{m}{s^2} = 5 \, \frac{m}{s}$
Por lo tanto, la velocidad del antílope al pasar por el primer punto era de $5 \, \frac{m}{s}$ (respuesta al ítem a) y su aceleración era de $1.43 \, \frac{m}{s^2}$ (respuesta al ítem b)
🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
