Volver a Guía
Ir al curso
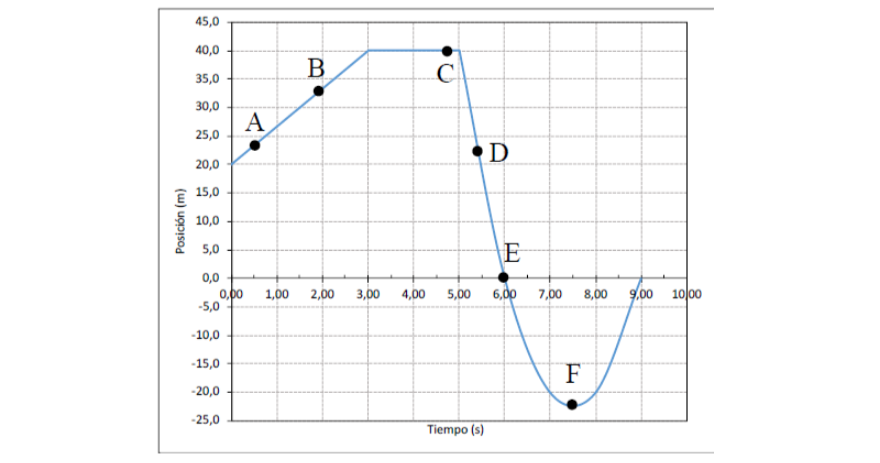
A partir del gráfico de posición en función del tiempo, tenemos que calcular la velocidad instantánea en cada uno de los puntos que nos marcan. Para eso, es clave recordar que, la velocidad en cada punto de la curva de posición en función del tiempo es la pendiente de la recta tangente en ese punto.
Reportar problema
CURSO RELACIONADO
Física 03
2026
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
2. Un automóvil de prueba viaja en linea recta a lo largo del eje $x$. La gráfica indica la posición $x$ del automóvil en función del tiempo. Obtenga la velocidad instantánea en cada uno de los puntos A a F.

Respuesta
💡 Aclaración: Para resolver este ejercicio, no sólo es importante que hayas visto primero las clases, sino que además vamos a usar explicitamente algunas ídeas muy básicas que se ven en Análisis y yo te mencioné en el repaso dentro del curso. De todas formas, si todavía no cursaste Análisis y por eso te resulta un poco raro, tranqui, nunca ví que tomaran algo así en el ejercicio de cinemática en los parciales de UBA XXI, y te prometo que estas ideas de a poco van a empezar a cerrar más.
Ahora sí, a resolverlo...
Vamos arrancar por los puntos más fáciles...
➡️ Viendo el gráfico, hay dos puntos muy fáciles donde a a ojo ya podemos ver cuánto vale la velocidad. Fijate que en los puntos C y F, la recta tangente a la curva tiene pendiente cero (la recta tangente es una recta horizontal). Entonces, como esa pendiente es cero, la velocidad en C y F es $0 \, \frac{m}{s}$.
Vamos con los otros...
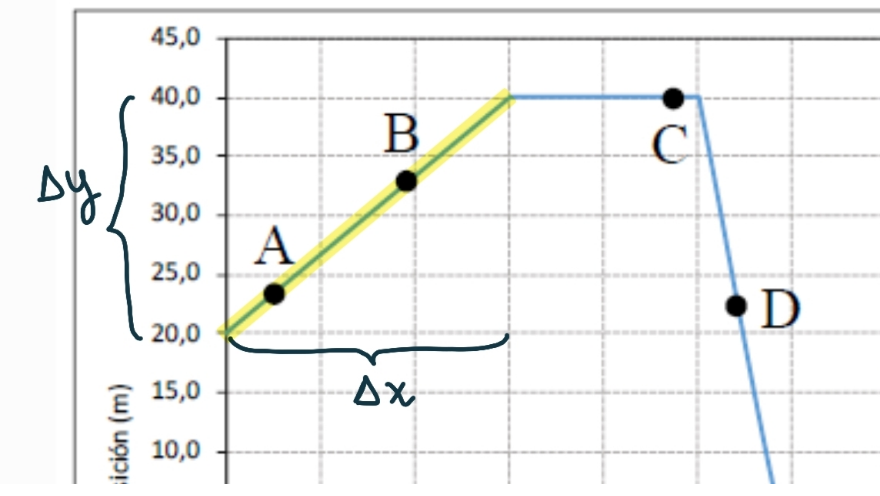
➡️ Los puntos A y B están sobre una recta (entre los 0 y 3 segundos, la curva de posición en función del tiempo es una recta). La pendiente de la recta tangente en esos puntos coincide con la pendiente de esa recta. A partir del gráfico, y usando lo que sabemos de función lineal, podemos calcular la pendiente $m$ de esa recta:
$m = \frac{\Delta y}{\Delta x} = \frac{20 \text{ m}}{3 \text{ s}} = 6.67 \, \frac{m}{s}$

Por lo tanto, la velocidad en los puntos A y B es $6.67 \, \frac{m}{s}$
➡️ En D y E nos pasa algo similar. Ambos puntos están sobre una recta (entre los 5 y 6 segundos el gráfico de posición en función del tiempo es esa recta con pendiente negativa) y la pendiente de la recta tangente va a coincidir con la pendiente de esa recta. Usando el mismo razonamiento, la pendiente es $-40 \, \frac{m}{s}$ (atenti, a diferencia del caso anterior, esta pendiente es negativa!) -> Por lo tanto, la velocidad en los puntos D y E es $-40 \, \frac{m}{s}$
🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
