Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2025
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
2.
Un pintor de $75,0 \mathrm{~kg}$ pinta una pared estando de pie sobre una tabla larga que descansa apoyada en dos puntos sobre un andamio, tal como lo muestra la figura. Si la tabla es homogénea y tiene una masa de 15,0 kilogramos, ¿cuán cerca del extremo izquierdo de la tabla podrá pararse sin que la tabla se incline?
Respuesta
💡 Importante: Para entender esta resolución es clave que primero hayas visto las clases de estática de cuerpo extenso, donde resolvemos vamos ejercicios de este estilo en video. Mi consejo es que veas primero las clases y resoluciones que aparecen en esa sección y después vengas a estos ejercicios de la guía, para seguir practicando.
Reportar problema
Arrancamos como siempre armándonos el diagrama de cuerpo libre del andamio con todas las fuerzas que están actuando en él:
A las fuerzas de contacto donde está apoyado el andamio las llamo $N_1$ y $N_2$, y tenemos también el peso del andamio $(P_A)$ y el peso de la persona $(P_P)$
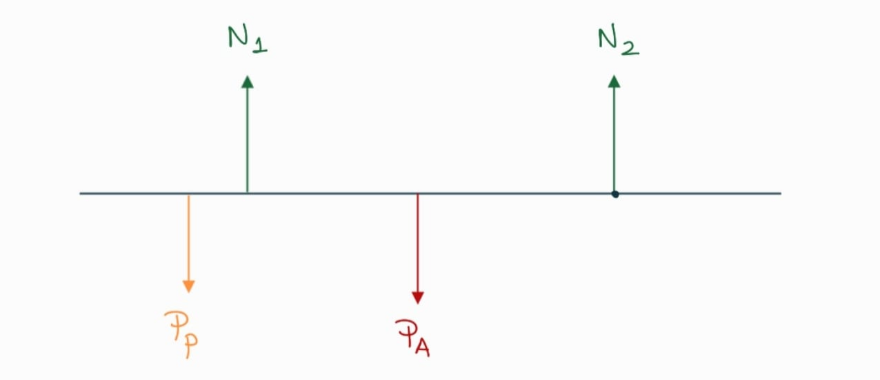
Pero acá hay algo fundamental que tenemos que tener en cuenta... Nosotros estamos analizando el caso límite, o sea, cuando el pintor se acercó tanto al extremo izquierdo que la tabla está a punto de desestabilizarse completamente y rotar 😅 ¿Te llegás a imaginar que, en esa situación límite, la $N_2$ ya no va a estar actuando?
Aclaración: Darte cuenta de esto, para mí, era lo más difícil de este problema y probablemente no sea para nada obvio al principio. Es muy parecido a lo que nos había pasado en el ejercicio de parcial de la barrera, donde también analizamos el caso límite donde queríamos abrir la barrera y, en ese escenario, ya no teníamos en cuenta una de las fuerzas de apoyo.
O sea, el diagrama de cuerpo libre del andamio para ese caso límite sería este:
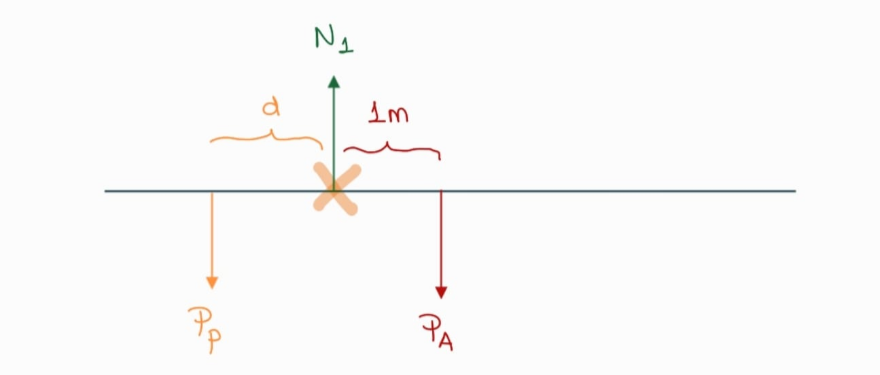
Ahí de paso ya te marqué cuál elegí como mi centro de momentos y la distancia de cada una de las fuerzas peso a ese centro de momentos (para deducir esas distancias usé el esquema del enunciado). Fijate que elegir el centro de momentos como el punto de aplicación de $N_1$ es muuuuy conveniente porque, al igual que ya nos pasó en otros ejercicios que resolvimos en los videos, esa fuerza no la conocemos ni nos interesa conocerla.
Calculamos ahora los momentos de cada fuerza:
👉 $|M_{P_A}| = d \cdot F_{\perp} = 1 \text{ m} \cdot P_A = 2 \text{ m} \cdot 15 \text{ kg} \cdot 9.8 \, \frac{m}{s^2} = 147 \text{ N} \cdot m$
Como esta fuerza me produce un giro en sentido horario, entonces le pongo signo negativo ➡️ $-147 \text{ N} \cdot m$
👉 $|M_{P_p}| = d \cdot F_{\perp} = d \cdot P_p = d \cdot 75 \text{ kg} \cdot 9.8 \, \frac{m}{s^2} = d \cdot 735 \text{ N}$
Como esta fuerza me produce un giro en sentido antihorario, entonces le pongo signo positivo ➡️ $d \cdot 735 \text{ N}$
Pedimos ahora que la suma de momentos respecto de $o$ sea cero, para que el andamio todavía esté en equilibrio:
$\sum M_{(o)} = 0$
$-147 \text{ N} \cdot m + d \cdot 735 \text{ N} = 0$
Despejamos $d$
$d = 0.2 \text{ m}$
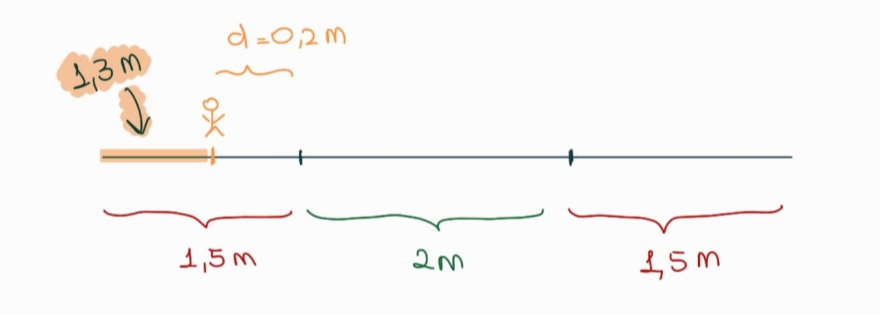
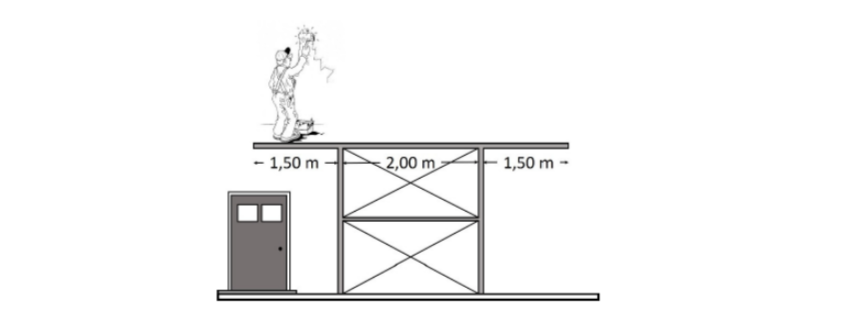
Pero atenti, que esta es la distancia al que elegimos como centro de momentos, nosotros necesitamos la distancia al extremo izquierdo. Entonces, usando el esquema del enunciado, nos damos cuenta que esa distancia que estamos buscando es $1.3 \text{ m}$. Va esquemita final por las dudas:
Iniciá sesión o
Registrate para
dejar
tu
comentario.
🤖 ExaBoti
Esta conversación es privada
🤖 ExaBoti (privado)