FÍSICA 03 CBC
CÁTEDRA ÚNICA
Final B (Julio 2025 ✨)
Ejercicio
1:
Dos automóviles A y B se desplazan por la misma carretera rectilínea pero en sentidos opuestos. El automóvil A circula a velocidad constante de $72 \text{ km/h}$, mientras que el automóvil B parte desde el reposo y acelera uniformemente a razón de $2 \text{ m/s}^2$. A los $5$ segundos de haber iniciado su movimiento, el automóvil B se cruza con el automóvil A.
a) ¿Qué distancia los separaba en el instante en que B comenzó a moverse?
$\square$ $75 \text{ m}$ $\square$ $125 \text{ m}$ $\square$ $150 \text{ m}$ $\square$ $300 \text{ m}$ $\square$ $450 \text{ m}$ $\square$ $600 \text{ m}$
b) El módulo de la velocidad media del móvil B entre $t = 5 \text{ s}$ y $t = 15 \text{ s}$ es:
$\square$ $0 \text{ km/h}$ $\square$ $18 \text{ km/h}$ $\square$ $36 \text{ km/h}$ $\square$ $54 \text{ km/h}$ $\square$ $72 \text{ km/h}$ $\square$ $90 \text{ km/h}$
Ejercicio
2:
Se lanza un proyectil en tiro oblicuo desde el origen de coordenadas con velocidad inicial de módulo $30 \text{ m/s}$ en una dirección que forma un cierto ángulo con la horizontal. Se desprecian todos los rozamientos.
a) ¿Cuál de las siguientes proposiciones es correcta?
$\square$ En la altura máxima su velocidad es nula
$\square$ Cuando vuelve al nivel de partida, el módulo de su velocidad es mayor que $30 \text{ m/s}$
$\square$ La aceleración cambia de sentido al llegar a la altura máxima
$\square$ El módulo de la velocidad toma su valor mínimo al llegar a la altura máxima
$\square$ La aceleración es nula al llegar a la altura máxima
$\square$ Existe una fuerza que lo impulsa en el sentido de la velocidad en todo momento
b) ¿Cuál es la altura máxima si el proyectil tardó $1$ segundo en alcanzarla?
$\square$ $2.5 \text{ m}$ $\square$ $5 \text{ m}$ $\square$ $7.5 \text{ m}$ $\square$ $10 \text{ m}$ $\square$ $12.5 \text{ m}$ $\square$ $15 \text{ m}$
Ejercicio
3:
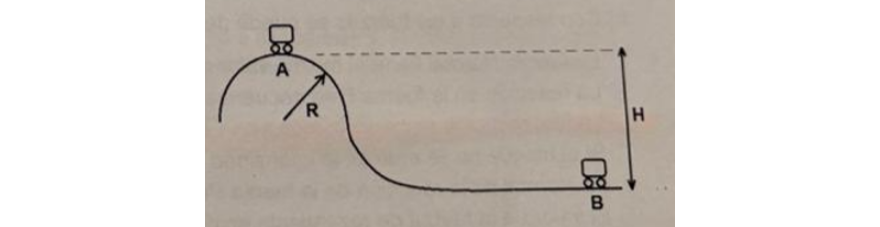
Un carrito de $60 \text{ kg}$ se desplaza por una montaña rusa y pasa por la parte más alta (punto A) de una vuelta vertical (una circunferencia en un plano vertical) de radio $R = 10 \text{ m}$, moviéndose en ese punto con una velocidad de módulo $9 \text{ m/s}$
a) ¿Cuánto vale el módulo de la fuerza que el carrito ejerce sobre la pista en ese instante?
$\square$ $0 \text{ N}$ $\square$ $60 \text{ N}$ $\square$ $114 \text{ N}$ $\square$ $360 \text{ N}$ $\square$ $600 \text{ N}$ $\square$ $1086 \text{ N}$
b) Si pasa por el punto B (H = 20 m) con velocidad cuyo módulo es de $20 \text{ m/s}$, el trabajo de las fuerzas no conservativas entre A y B vale:
$\square$ $0 \text{ J}$ $\square$ $-545 \text{ J}$ $\square$ $-1920 \text{ J}$ $\square$ $-2430 \text{ J}$ $\square$ $-2840 \text{ J}$ $\square$ $-3560 \text{ J}$
Ejercicio
4:
Un satélite artificial orbita la Tierra a una distancia de $4 \times 10^4 \text{ km}$ del centro del planeta.
a) ¿Cuál es aproximadamente su período orbital en horas?
Datos: $G = 6.67 \times 10^{-11} \, \frac{N \cdot m^2}{kg^2}$, masa de la Tierra $M_T = 6 \times 10^{24} \text{ kg}$
$\square$ $3$ $\square$ $8$ $\square$ $13$ $\square$ $22$ $\square$ $43$ $\square$ $51$
b) Si un segundo satélite artificial orbita la Tierra a una distancia que es la mitad de la del primer satélite, ¿cómo se relacionan los módulos de sus velocidades tangenciales?
$\square$ $v_{t2} = v_{t1}$
$\square$ $v_{t2} = v_{t1}/2$
$\square$ $v_{t2} = \sqrt{2} \, v_{t1}$
$\square$ $v_{t2} = v_{t1} / \sqrt{2}$
$\square$ $v_{t2} = 2 \, v_{t1}$
$\square$ $v_{t2} = 4 \, v_{t1}$
Ejercicio
5:
Un cubo de madera, de arista $a = 20 \text{ cm}$, flota en el agua con el 60% de su volumen sumergido. Si la densidad del agua es $1000 \text{ kg/m}^3$
a) ¿Cuánto vale la fuerza de empuje que el agua ejerce sobre el cubo?
$\square$ $12 \text{ N}$ $\square$ $24 \text{ N}$ $\square$ $36 \text{ N}$ $\square$ $42 \text{ N}$ $\square$ $48 \text{ N}$ $\square$ $56 \text{ N}$
b) ¿Qué masa $m$ hay que colocar sobre el cubo para que este último quede flotando con su superficie superior al ras del agua?
$\square$ $1.8 \text{ kg}$ $\square$ $2.2 \text{ kg}$ $\square$ $2.8 \text{ kg}$ $\square$ $3.2 \text{ kg}$ $\square$ $3.8 \text{ kg}$ $\square$ $4.2 \text{ kg}$
Ejercicio
6:
Sobre un bloque en reposo de masa $M = 4 \text{ kg}$ se aplica una fuerza $F$ de módulo $20 \text{ N}$ como se muestra en la figura. Los coeficientes de rozamiento son $\mu_e = 0.8$ y $\mu_d = 0.3$
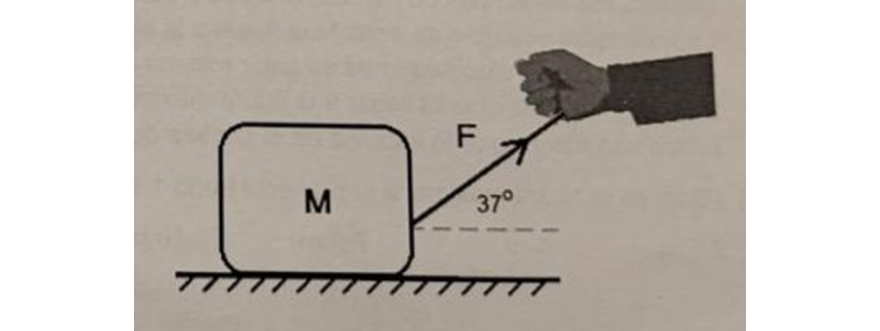
a) En esas condiciones se puede asegurar que el bloque:
$\square$ No se mueve y la fuerza de rozamiento vale $32 \text{ N}$
$\square$ No se mueve y la fuerza de rozamiento vale $22.4 \text{ N}$
$\square$ No se mueve y la fuerza de rozamiento vale $16 \text{ N}$
$\square$ Se mueve y la fuerza de rozamiento vale $15.6 \text{ N}$
$\square$ Se mueve y la fuerza de rozamiento vale $12 \text{ N}$
$\square$ Se mueve y la fuerza de rozamiento vale $8.4 \text{ N}$
b) Con respecto a las fuerzas se puede decir que:
$\square$ La fuerza normal tiene el mismo valor que la fuerza peso
$\square$ La reacción de la fuerza $F$ se encuentra en el piso
$\square$ La fuerza que la mano transmite hacia el bloque es igual a la que el bloque transmite hacia la mano
$\square$ Si el bloque no se mueve, la intensidad de la fuerza de rozamiento es igual a la de $F$
$\square$ La normal es la reacción de la fuerza peso
$\square$ El valor de la fuerza de rozamiento no depende del ángulo que la fuerza $F$ forma con la horizontal



