Valores de seno y coseno que tenés que saber💡
A continuación te dejo algunos valores típicos del seno y del coseno para diferentes ángulos, que tenés que recordar para cuando vayas a rendir.
✅ Si viste los videos de la circunferencia trigonométrica, probablemente puedas deducirlos simplemente armandote una circunferencia en tu hoja, sin que haga falta que memorices nada✨
| $x$ 👉 | $0$ | $\dfrac{\pi}{6}$ | $\dfrac{\pi}{4}$ | $\dfrac{\pi}{3}$ | $\dfrac{\pi}{2}$ | $\pi$ | $\dfrac{3}{2}\pi$ |
$2\pi$ |
|---|---|---|---|---|---|---|---|---|
| $y = sen(x)$ | $0$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{\sqrt{3}}{2}$ | $1$ | $0$ | $-1$ | $0$ |
| $x = cos(x)$ | $1$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{\sqrt{2}}{2}$ | $\dfrac{1}{2}$ | $0$ | $-1$ | $0$ | $1$ |
💡Notá que los valores de $x$ son ángulos, medidos en radianes, y por eso tienen siempre $\pi$. Mientras que los valores del seno y del coseno no tienen $\pi$.
¿Cómo los vamos a usar en los ejercicios?
👉 Cuando nos pidan calcular el valor de seno o coseno para un determinado ángulo $x$ (lo que vemos en la tabla)
Ejemplo: Calcular el $\sin(x)$ para $x = \dfrac{\sqrt{3}}{2}$.
Recordando la tabla, vemos que la solución es el ángulo $x = \dfrac{\pi}{3}$
👉 O cuando nos den el valor del seno o del coseno y nos pidan hallar el / los ángulos que son solución de esa ecuación.
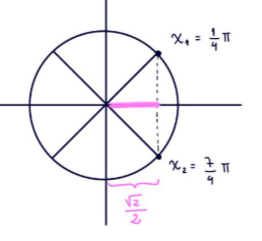
Ejemplo: Hallar los valores de $x$ que verifican que $\cos(x)=\frac{\sqrt{2}}{2}$.
Recordando la tabla, vemos que el valor de $x$ que verifica que $\cos(x)=\frac{\sqrt{2}}{2}$ es el ángulo $x = \dfrac{\pi}{4}$. Peeeero ¡alto ahí! SIEMPRE, pero SIEMPRE que tengas que hallar valores de $x$ (ángulos), tenés que verificar que no haya otro valor de$x$ que también cumpla esa condición. Y para eso vas a usar la circunferencia trigonométrica.
En este caso, no solamente el ángulo $x = \dfrac{\pi}{4}$ hace que $\cos(x)=\frac{\sqrt{2}}{2}$; sino que el ángulo $x = \dfrac{7\pi}{4}$ también es otra solución posible.

Las soluciones de la ecuación $\cos(x)=\frac{\sqrt{2}}{2}$, son:
$x_1 = \dfrac{\pi}{4}$ y $x_2 = \dfrac{\pi}{4}$
Pero estas soluciones no son todas las posibles, solamente son las soluciones que están dentro de un pequeño intervalo que va de $[0, 2\pi]$
¿Cómo podemos encontrar todas las soluciones posibles de esta ecuación? (Spoiler: son infinitas)
Eso lo que vamos a ver a continuación, porque es lo que más toman de este tema😉

$cos(\frac{\pi}{2}) = 0$
Para saber qué valor de seno y coseno corresponde a cada ángulo, tenés que ver los videos de la circunferencia trigonométrica del curso.
Confirmar eliminación
¿Estás segurx de que quieres eliminar esta respuesta? Esta acción no se puede deshacer.
Confirmar eliminación
¿Estás segurx de que quieres eliminar este comentario? Esta acción no se puede deshacer.